1. Basic concepts

  • Statistics: The process of drawing conclusions for a population based on limited data

  • Population and Sample

    • Population (모집단): A complete set of items
    • Sample (표본집단): A subset of individuals
    • We acquire data from the population as samples and draw conclusions.

2. Sampling Noise

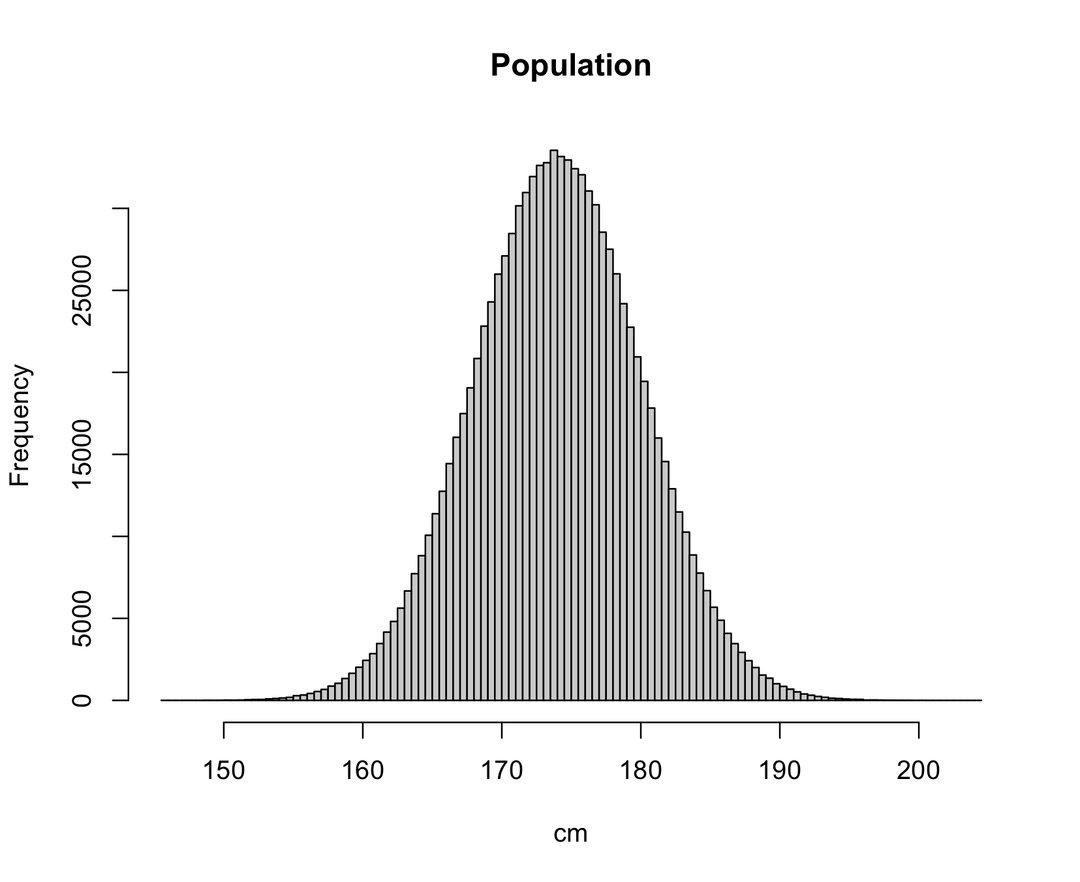
모집단 population을 평균이 174, 표준편차가 6이고 크기가 1,000,000인 정규분포라고 해보자. 간격을 1로 설정한 히스토그램을 생성하면 아래와 같다.

# Population
set.seed(100)
population <- rnorm(n = 1000000, mean = 174, sd = 6)
hist(population, breaks = 100, xlab = "cm")

set.seed() 함수는 난수를 생성하는 경우에 출발점(seed)을 고정함으로써 항상 동일한 결과가 나오게 한다. 만약 이 함수를 사용하지 않는다면, 코드를 실행할 때마다 다른 결과가 나올 것이다. 함수 안에 들어가는 인수는 0 이상의 아무 정수나 넣어주면 되고, 이 인수가 달라지면 난수 생성 결과가 달라진다.

Alt text

모집단에서 크기가 50인 표본을 추출해보자. 이때 R에 내장된 sample() 함수를 이용할 것이다.

sample(x, size): x 벡터에서 size번 만큼 비복원 무작위 추출

1부터 1,000,000까지의 정수 중 50개를 무작위 추출한 것을 a1a_1, a2a_2, …, a50a_{50} 이라고 하자. 모집단 population의 ana_n번째 수를 모은 것을 smpl.height에 저장하고 히스토그램을 만든다.

# Sample
smpl.idx <- sample(1:1000000, 50)
smpl.height <- population[smpl.idx]
hist(smpl.height, breaks = 100, xlab = "cm")

R 언어에서는 변수명에 period

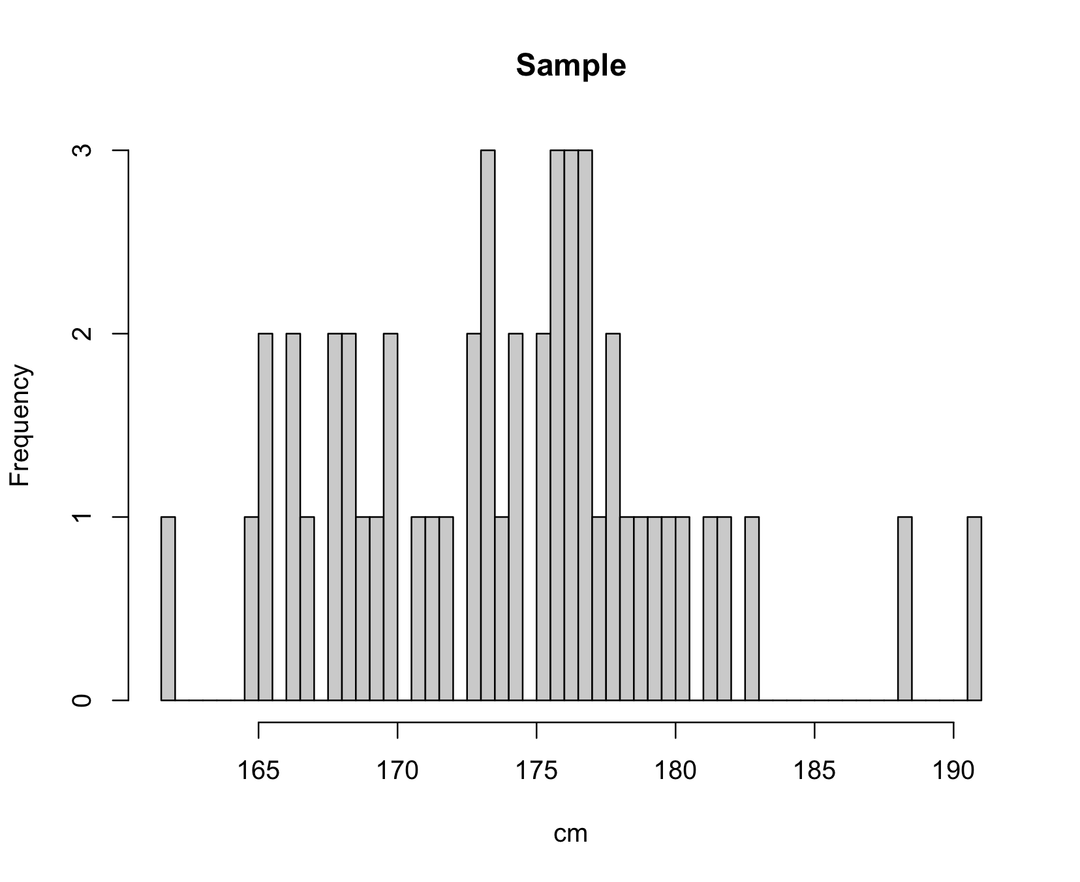
Alt text

표본집단의 히스토그램 모양이 모집단의 그것과 상이하다고 할 수 있다. 이것을 Sampling Noise라고 하며, 표본 크기가 작을수록 커진다.